Quantum numbers: What they are, exercises and examples

According to Niels Bohr's atomic model, the protons and neutrons of an atom are in the nucleus, while the electrons are around it. Although we cannot know where an electron is exactly, there are areas where it is most likely to be found, the atomic orbitals. And how can we determine those orbitals? Very simple, using quantum numbers.

What are the quantum numbers?

There are 4 quantum numbers. Three of them give us information about where an electron of a certain atom is, that is, they give us information about the orbital. On the other hand, the fourth quantum number does not tell us where the electron is, but how. Are you still not very clear about this? Go for it!

Principal quantum number (n). It is the last energy level to fill and indicates the size of the orbital and therefore the distance between the nucleus and the electron. Why? Very easy. The larger the orbital, the further the electron can be from the nucleus of the atom.
Azimuthal or secondary quantum number (l). Indicate the shape of the orbital.
Magnetic quantum number (m). Indicates the orientation of the orbital.
Spin quantum number (s). Tell which way the electron rotates.

Easy right? Let's go with the important thing!

How are quantum numbers derived

To get the quantum numbers you just have to follow 2 simple steps:

Write the electron configuration.
Get the quantum numbers from the differential electron (the last one that fills the orbital).

Electronic configuration

We start with step 1, write the electron configuration. How? There are two methods to do it, let's get to it!

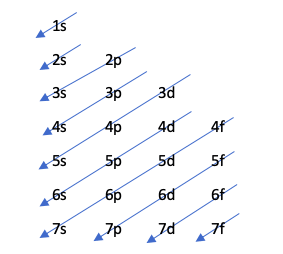
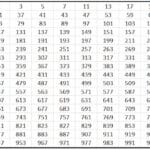
Moeller diagram

This technique indicates the order of filling of the orbitals through the following drawing:

This diagram is governed by the Aufbau principle, which defends that the orbitals fill in increasing order of energy, that is, the orbital that has the least energy will fill up earlier.

To find out which orbital has more energy, the operation n + l is performed. If this operation for two different atoms results in the same number, the one whose number n is higher will have more energy. In other words, in case of a tie, the one with the lowest number n is filled first. Let's see it with an example:

4p: n + l -> 4 + 1 = 5

5s: n + l -> 5 + 0 = 5

As there is a tie in the n + l rule, it fills 4p earlier because its number n is lower.

Kernel Model

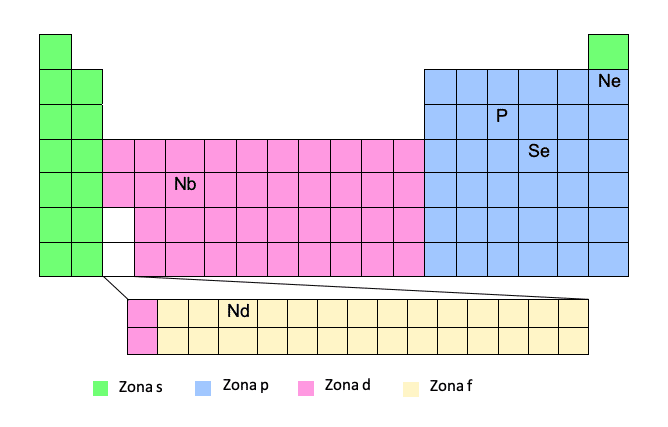
To get the electronic configuration following this model you must know the periodic table very well. If we have the atomic number and position of the element in the table, it is a piece of cake!

This method is considered a simplified method since it allows not having to write the complete electron configuration. In this way, we can write the name of the noble gas element above in brackets, and then the path from that noble gas to the element in question. Let's see an example:Thus, we will write the trajectory taking into account the number of the period (row of the periodic table) and the "zone" and, once the electronic configuration is written, we will extract the quantum numbers.

The phosphor (P) will be written from the previous noble gas, that is, Neon:

P -> [Ne] 3s²3p³

Of course, you have to be careful with this method, since zones d and f are special zones. As we make the journey, in zone d we will not put the number of the period (row), but the number of the period minus one. The same happens with area F, we will not put the number of the period, but the number of the period minus two. You will understand it better with a couple of examples:

Nb -> [Kr] 5s¹4d⁴

Although it is in period 5, when we are in zone d, we subtract 1.

Nd -> [Xe] 6s²4f¹⁴

Although it is in period 6, when we are in zone f, we subtract 2.

Exceptions in the electronic configuration

The electron configuration has a couple of special aspects that, if you are not aware of them, can cause you large head feeders. But do not spread panic! We will tell you!

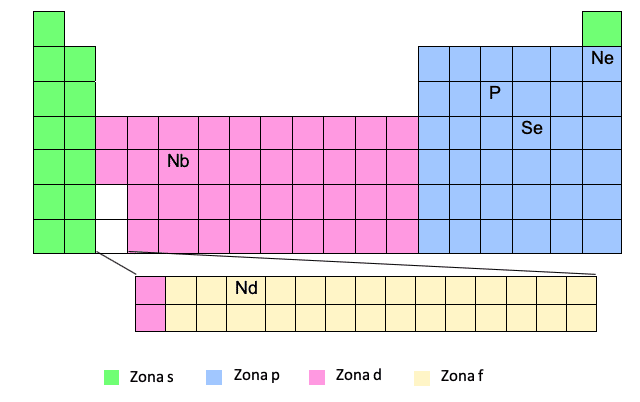
Zone F

Zone F appears at the bottom of the periodic table, but is actually "embedded" in the gap that we see in white, that is, between the first and second elements of the last two rows of zone D.

You see it? Therefore, sometimes, when we have to write the electronic configuration of an element in zone F, for example, Nd, we will have to put an electron in zone D of the corresponding level in reference to that element in zone D that is before entering zone F.

Ce -> [Xe] 6s²5d¹4f¹

Group 6 and Group 11

The group 6 and group 11 transition metals have 4 and 9 electrons in their last shells, respectively. Therefore, to be a more stable element, the s orbital becomes excited and loses an electron, which passes to the next orbital, the d. In this way, the s orbital will be left with an electron; and d with 5, if it is an element of group 6, or with 10, if it is an element of group 11.

Here's an example:

Ag -> [Kr] 5s²4d⁹

Apparently, this would be the electron configuration of silver (Ag). However, losing an electron from the s orbital, it looks like this:

Ag -> [Kr] 5s¹4d¹⁰

However, there are exceptions to this rule, such as Tungsten (group 6), which is left with 2 electrons in the s orbital and 4 in the d orbital.

But don't worry! The most typical ones (Cr, Cu, Ag and Au) do follow this rule.

Do you get it? Well. That's all you need to know about electron configuration. Let's go for quantum numbers!

How to get quantum numbers

In order to get the quantum numbers, we must know how many electrons fit in each orbital shell, taking into account that 2 electrons fit in an orbital.

Layer s. It has only one orbital, so it can hold 2 electrons.

Layer p. It has 3 orbitals, so there is room for 6 electrons.

Layer d. It has 5 orbitals, so it can hold 10 electrons.

Layer f. It has 7 orbitals, that is, it can hold 14 electrons.

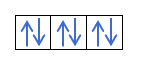
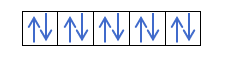
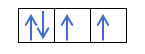
Now that you understand that there are 2 electrons in each orbital, you should know Hund's rule. This rule says that when filling orbitals of the same sublevel or shell, for example, the p shell, the electrons fill the orbital in one direction (positive) and then in the other (negative). Do you want to see it with an example?

If we have 2p⁴, that is, the 2p orbital with 4 electrons, will not fill like this:

It will fill like this:

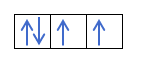
Are you getting it? Great, let's see how to calculate the numbers:

Quantum number n. This number coincides with the number of the last level of the electron configuration. For example, if the electron configuration ends in 4s², the principal quantum number will be 4.
Quantum number l. This number depends on the last layer that has been filled.
Layer s -> l = 0
Layer p -> l = 1
Layer d -> l = 2
Layer f -> l = 3
Quantum number m. The number m can be any value between -l to + l, so it will depend on the sublevel in which the differential electron is, that is, on whether it is s, p, d or f. How to calculate this number is a bit more complicated, let's see it with a couple of drawings:
Layer s -> As we have seen, the l is worth 0, so the m can only be worth 0.
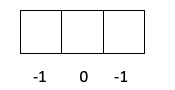
Layer p -> The l is worth 1, so the m can be -1, 0 or 1.

Layer d -> The l is 2, so the m could be -2, -1, 0, 1 and 2.

Layer f -> The l is worth 3, so m can be -3, -2, -1, 0, 1, 2 and 3.

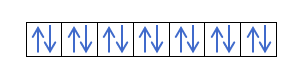
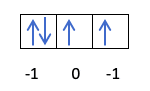
You already know how the orbitals are filled, so the quantum number m will have the value of the hole where the last drawn electron is. Do you remember this example from before ?:

In this case, the m will be -1, since in the p shell (3 orbitals), if there are 4 electrons, the last one to fill would be the negative of the first orbital.

Quantum number s. The quantum number s can only be worth ½ and -½. If the last electron drawn is positive, that is, the arrow is up, the s will be ½. On the other hand, if the last electron to fill the orbital is negative, that is, with the arrow pointing down, the s will be -½.

Exercises and examples

Yes, we already know that all this is a lot of information, but you will understand it better with some examples. Here we go!

Example 1

Selenium (Se) -> Atomic number: 34

We write the electron configuration. We are writing the electron configuration according to the Moeller diagram, taking into account that the s, p, d and f orbitals have 2, 6, 10 and 14 electrons respectively. We are writing the configuration by adding the number of electrons, which is written as an exponent.

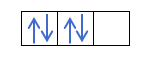
1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁴

As the 4p orbital does not fill, since the electrons would add up to 36, we do not put 4p⁶but 4p⁴.

We take out the quantum numbers. To do this, we look at the valence or differential electron, that is, the last electron that has filled the orbital. In this case, we will look at 4p⁴.
- Principal quantum number. The last energy level to fill was 4.

n = 4