ક્વોન્ટમ નંબરો: તેઓ શું છે, કસરતો અને ઉદાહરણો

નીલ્સ બોહરના અણુ મોડેલ મુજબ, અણુના પ્રોટોન અને ન્યુટ્રોન ન્યુક્લિયસમાં હોય છે, જ્યારે ઇલેક્ટ્રોન તેની આસપાસ હોય છે. જોકે આપણે જાણી શકતા નથી કે ઇલેક્ટ્રોન બરાબર ક્યાં છે, ત્યાં એવા વિસ્તારો છે જ્યાં તે મળવાની શક્યતા છે, અણુ ભ્રમણકક્ષાઓ. અને આપણે તે ભ્રમણકક્ષા કેવી રીતે નક્કી કરી શકીએ? ખૂબ સરળ, ક્વોન્ટમ સંખ્યાઓનો ઉપયોગ કરીને.

ક્વોન્ટમ સંખ્યાઓ શું છે?

ત્યાં 4 ક્વોન્ટમ સંખ્યાઓ છે. તેમાંના ત્રણ આપણને ચોક્કસ અણુનું ઇલેક્ટ્રોન ક્યાં સ્થિત છે તે વિશે માહિતી આપે છે, એટલે કે, તેઓ અમને ભ્રમણકક્ષા વિશે માહિતી આપે છે. બીજી બાજુ, ચોથો ક્વોન્ટમ નંબર આપણને કહેતો નથી કે ઇલેક્ટ્રોન ક્યાં છે, પરંતુ કેવી રીતે. શું તમે હજી પણ આ વિશે સ્પષ્ટ નથી? તેના માટે જાઓ!

મુખ્ય ક્વોન્ટમ નંબર (એન). તે ભ્રમણ કરવા માટેનું છેલ્લું ઉર્જા સ્તર છે અને ભ્રમણકક્ષાનું કદ સૂચવે છે અને તેથી ન્યુક્લિયસ અને ઇલેક્ટ્રોન વચ્ચેનું અંતર. કેમ? અત્યંત સરળ. ભ્રમણકક્ષા જેટલી મોટી છે, ઇલેક્ટ્રોન અણુના ન્યુક્લિયસથી વધુ આગળ વધી શકે છે.
અઝીમુથલ અથવા ગૌણ ક્વોન્ટમ નંબર (એલ). ભ્રમણકક્ષાનો આકાર સૂચવો.
ચુંબકીય ક્વોન્ટમ નંબર (મી). ભ્રમણકક્ષાની દિશા સૂચવે છે.
સ્પિન ક્વોન્ટમ નંબર (ઓ). ઇલેક્ટ્રોન કઈ રીતે ફરે છે તે કહો.

સરળ અધિકાર? ચાલો અગત્યની વાત સાથે જઈએ!

ક્વોન્ટમ સંખ્યાઓ કેવી રીતે પ્રાપ્ત થાય છે

ક્વોન્ટમ નંબરો મેળવવા માટે તમારે ફક્ત 2 સરળ પગલાંને અનુસરવું પડશે:

ઇલેક્ટ્રોન રૂપરેખાંકન લખો.
વિભેદક ઇલેક્ટ્રોન (છેલ્લા જે ભ્રમણકક્ષા ભરે છે) માંથી ક્વોન્ટમ સંખ્યા મેળવો.

ઇલેક્ટ્રોનિક રૂપરેખાંકન

અમે પગલું 1 થી પ્રારંભ કરીએ છીએ, ઇલેક્ટ્રોન રૂપરેખાંકન લખો. કેવી રીતે? તે કરવા માટે બે પદ્ધતિઓ છે, ચાલો તેને મેળવીએ!

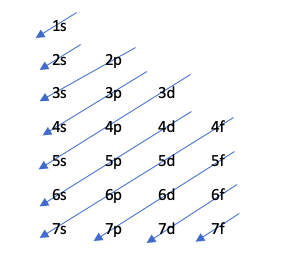
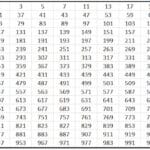
મોએલર ડાયાગ્રામ

આ તકનીક નીચેના ચિત્ર દ્વારા ભ્રમણકક્ષાઓ ભરવાનો ક્રમ સૂચવે છે:

આ આકૃતિ આફબાઉ સિદ્ધાંત દ્વારા સંચાલિત છે, જે બચાવ કરે છે કે ભ્રમણકક્ષા energyર્જાના વધતા ક્રમમાં ભરે છે, એટલે કે, ભ્રમણકક્ષા કે જે ઓછામાં ઓછી energyર્જા ધરાવે છે તે અગાઉ ભરાશે.

કયા ભ્રમણકક્ષામાં વધુ energyર્જા છે તે શોધવા માટે, ઓપરેશન n + l કરો. જો બે અલગ અલગ અણુઓ માટે આ ઓપરેશન એક જ સંખ્યામાં પરિણમે છે, જેની સંખ્યા n વધારે છે તેની પાસે વધુ haveર્જા હશે. બીજા શબ્દોમાં કહીએ તો, ટાઇની સ્થિતિમાં, સૌથી નીચો નંબર n ધરાવતી વ્યક્તિ પ્રથમ ભરાય છે. ચાલો તેને એક ઉદાહરણ સાથે જોઈએ:

4p: n + l -> 4 + 1 = 5

5s: n + l -> 5 + 0 = 5

N + l નિયમમાં ટાઇ હોવાથી, તે 4p અગાઉ ભરે છે કારણ કે તેની સંખ્યા n ઓછી છે.

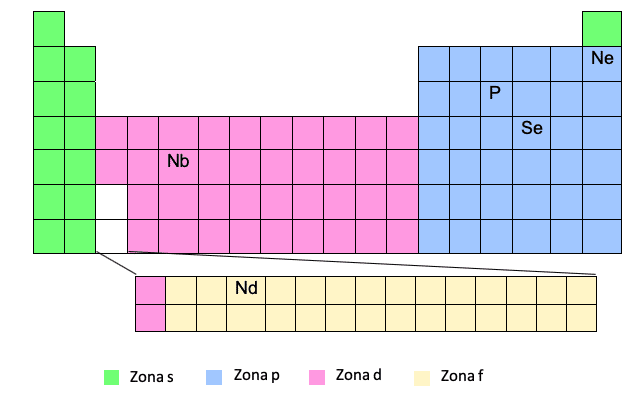
કર્નલ મોડેલ

આ મોડેલને અનુસરીને ઇલેક્ટ્રોનિક રૂપરેખાંકન મેળવવા માટે તમારે સામયિક કોષ્ટકને ખૂબ સારી રીતે જાણવું જોઈએ. જો આપણી પાસે કોષ્ટકમાં અણુ નંબર અને તત્વની સ્થિતિ છે, તો તે કેકનો ટુકડો છે!

આ પદ્ધતિ એક સરળ પદ્ધતિ માનવામાં આવે છે કારણ કે તે સંપૂર્ણ ઇલેક્ટ્રોન રૂપરેખાંકન લખવાની મંજૂરી આપતી નથી. આ રીતે, આપણે ઉપરના ઉમદા ગેસ તત્વનું નામ કૌંસમાં લખી શકીએ છીએ, અને પછી તે ઉમદા ગેસથી પ્રશ્નના તત્વ સુધીનો માર્ગ. ચાલો એક ઉદાહરણ જોઈએ:આમ, અમે સમયગાળાની સંખ્યા (સામયિક કોષ્ટકની પંક્તિ) અને "ઝોન" ને ધ્યાનમાં રાખીને પ્રક્ષેપણ લખીશું અને, એકવાર ઇલેક્ટ્રોનિક રૂપરેખાંકન લખવામાં આવશે, અમે ક્વોન્ટમ સંખ્યાઓ કા extractીશું.

ફોસ્ફર (પી) અગાઉના ઉમદા ગેસમાંથી લખવામાં આવશે, એટલે કે નિયોન:

પી -> [ને] 3 સે²3p³

અલબત્ત, તમારે આ પદ્ધતિથી સાવચેત રહેવું જોઈએ, કારણ કે ઝોન ડી અને એફ ખાસ ઝોન છે. જેમ આપણે મુસાફરી કરીએ છીએ, ઝોન ડીમાં આપણે સમયગાળાની સંખ્યા (પંક્તિ) નહીં, પરંતુ સમયગાળાની સંખ્યા માઇનસ એક મૂકીશું. ક્ષેત્ર F સાથે પણ આવું જ થાય છે, અમે સમયગાળાની સંખ્યા મૂકીશું નહીં, પરંતુ સમયગાળાની સંખ્યા બાદબાકી બે. તમે તેને બે ઉદાહરણો સાથે વધુ સારી રીતે સમજી શકશો:

Nb -> [Kr] 5 સે¹4d⁴

જો કે તે સમયગાળા 5 માં છે, જ્યારે આપણે ઝોન ડીમાં છીએ, ત્યારે આપણે 1 બાદ કરીએ છીએ.

એનડી -> [Xe] 6 સે²4f¹⁴

જોકે તે સમયગાળા 6 માં છે, જ્યારે આપણે ઝોન f માં હોઈએ છીએ, ત્યારે આપણે 2 બાદ કરીએ છીએ.

ઇલેક્ટ્રોનિક રૂપરેખાંકનમાં અપવાદો

ઇલેક્ટ્રોન રૂપરેખાંકનમાં કેટલાક ખાસ પાસાં છે જે, જો તમે તેમને જાણતા નથી, તો મોટા હેડ ફીડર તરફ દોરી શકે છે. પરંતુ ગભરાટ ફેલાવો નહીં! અમે તમને કહીશું!

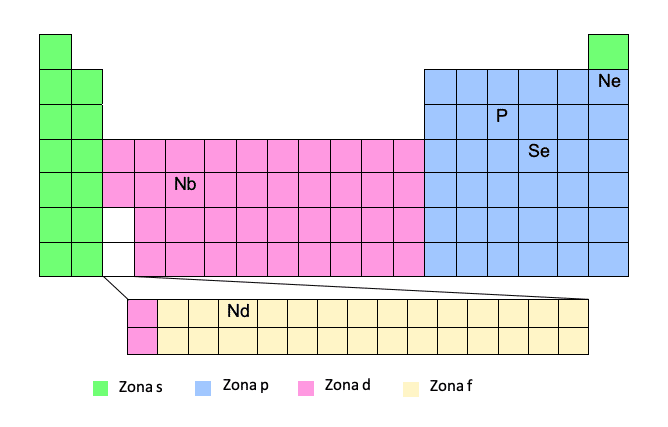
ઝોન એફ

સામયિક કોષ્ટકના તળિયે ઝોન એફ દેખાય છે, પરંતુ વાસ્તવમાં તે અંતરમાં "જડિત" છે જે આપણે સફેદ રંગમાં જોઈએ છીએ, એટલે કે, ઝોન ડીની છેલ્લી બે પંક્તિઓના પ્રથમ અને બીજા તત્વો વચ્ચે.

તમે તે જોયું? આ કારણોસર, કેટલીકવાર, જ્યારે આપણે ઝોન F માં કોઈ તત્વનું ઇલેક્ટ્રોનિક રૂપરેખાંકન લખવું પડે, ઉદાહરણ તરીકે, Nd, આપણે ઝોન D માં તે તત્વના સંદર્ભમાં સંબંધિત સ્તરના ઝોન D માં ઇલેક્ટ્રોન મૂકવું પડશે. ઝોન F માં પ્રવેશતા પહેલા.

Ce -> [Xe] 6 સે²5d¹4f¹

ગ્રુપ 6 અને ગ્રુપ 11

ગ્રુપ 6 અને ગ્રુપ 11 ટ્રાન્ઝિશન મેટલ્સ અનુક્રમે 4 અને 9 ઇલેક્ટ્રોન ધરાવે છે. તેથી, વધુ સ્થિર તત્વ બનવા માટે, ઓ ઓર્બિટલ ઉત્સાહિત થાય છે અને ઇલેક્ટ્રોન ગુમાવે છે, જે આગામી ઓર્બિટલમાં જાય છે, ડી. આ રીતે, ઓ ઓર્બિટલ ઇલેક્ટ્રોન સાથે બાકી રહેશે; અને d સાથે 5, જો તે જૂથ 6 નું તત્વ છે, અથવા 10 સાથે, જો તે જૂથ 11 નું તત્વ છે.

અહીં એક ઉદાહરણ છે:

Ag -> [Kr] 5 સે²4d⁹

દેખીતી રીતે, આ ચાંદી (એજી) નું ઇલેક્ટ્રોન રૂપરેખાંકન હશે. જો કે, જ્યારે ઓર્બિટલમાંથી ઇલેક્ટ્રોન ગુમાવવું, તે આના જેવો દેખાય છે:

Ag -> [Kr] 5 સે¹4d¹⁰

જો કે, આ નિયમમાં અપવાદો છે, જેમ કે ટંગસ્ટન (જૂથ 6), જે s ઓર્બિટલમાં 2 ઇલેક્ટ્રોન અને ડી ઓર્બિટલમાં 4 બાકી છે.

પરંતુ ચિંતા કરશો નહીં! સૌથી સામાન્ય (Cr, Cu, Ag અને Au) આ નિયમનું પાલન કરે છે.

તને મળે છે? વેલ. ઇલેક્ટ્રોન ગોઠવણી વિશે તમારે એટલું જ જાણવાની જરૂર છે. ચાલો ક્વોન્ટમ સંખ્યાઓ પર જઈએ!

ક્વોન્ટમ સંખ્યાઓ કેવી રીતે મેળવવી

ક્વોન્ટમ નંબરો મેળવવા માટે, આપણે જાણવું જોઈએ કે ભ્રમણકક્ષામાં 2 ઇલેક્ટ્રોન ફિટ છે તે ધ્યાનમાં લેતા, દરેક ભ્રમણકક્ષામાં કેટલા ઇલેક્ટ્રોન ફિટ છે.

સ્તર s. તે માત્ર એક ભ્રમણકક્ષા ધરાવે છે, તેથી તે 2 ઇલેક્ટ્રોન પકડી શકે છે.

સ્તર પી. તેમાં 3 ભ્રમણકક્ષાઓ છે, તેથી 6 ઇલેક્ટ્રોન માટે જગ્યા છે.

લેયર ડી. તેમાં 5 ભ્રમણકક્ષાઓ છે, તેથી તે 10 ઇલેક્ટ્રોન રાખી શકે છે.

સ્તર એફ. તેમાં 7 ભ્રમણકક્ષાઓ છે, એટલે કે, તે 14 ઇલેક્ટ્રોન રાખી શકે છે.

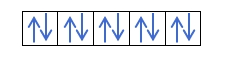
હવે તમે સમજો છો કે દરેક ભ્રમણકક્ષામાં 2 ઇલેક્ટ્રોન છે, તમારે હંડનો નિયમ જાણવો જોઈએ. આ નિયમ કહે છે કે જ્યારે સમાન સબલેવલ અથવા શેલના ભ્રમણકક્ષાઓ ભરીને, ઉદાહરણ તરીકે, p શેલ, ઇલેક્ટ્રોન ભ્રમણકક્ષાને એક દિશામાં (હકારાત્મક) અને પછી બીજી (નકારાત્મક) માં ભરે છે. શું તમે તેને ઉદાહરણ સાથે જોવા માંગો છો?

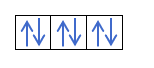
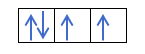
જો આપણી પાસે 2 પી⁴, એટલે કે, 2p ઇલેક્ટ્રોન સાથે 4p ભ્રમણકક્ષા, આ રીતે ભરાશે નહીં:

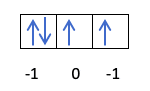
તે આ રીતે ભરાશે:

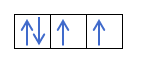
શું તમે તેને મેળવી રહ્યા છો? સરસ, ચાલો જોઈએ કે સંખ્યાઓની ગણતરી કેવી રીતે કરવી:

ક્વોન્ટમ નંબર n. આ સંખ્યા ઇલેક્ટ્રોન ગોઠવણીના છેલ્લા સ્તરની સંખ્યા સાથે એકરુપ છે. ઉદાહરણ તરીકે, જો ઇલેક્ટ્રોન રૂપરેખાંકન 4s માં સમાપ્ત થાય², મુખ્ય ક્વોન્ટમ નંબર 4 હશે.
ક્વોન્ટમ નંબર એલ. આ સંખ્યા છેલ્લા સ્તર પર ભરેલી છે તેના પર આધાર રાખે છે.
સ્તર s -> l = 0
સ્તર p -> l = 1
સ્તર d -> l = 2
સ્તર f -> l = 3
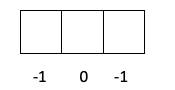
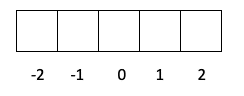
ક્વોન્ટમ નંબર મી. સંખ્યા m એ -l થી + l વચ્ચેનું કોઈપણ મૂલ્ય હોઈ શકે છે, તેથી તે સબલેવલ પર આધાર રાખે છે જેમાં વિભેદક ઇલેક્ટ્રોન છે, એટલે કે તે s, p, d અથવા f છે કે નહીં. આ સંખ્યાની ગણતરી કેવી રીતે કરવી તે થોડી વધુ જટિલ છે, ચાલો તેને થોડા ડ્રોઇંગ સાથે જોઈએ:
સ્તર s -> જેમ આપણે જોયું છે, l ની કિંમત 0 છે, તેથી m માત્ર 0 ની કિંમતનું હોઈ શકે છે.
સ્તર p -> l ની કિંમત 1 છે, તેથી m -1, 0 અથવા 1 હોઈ શકે છે.

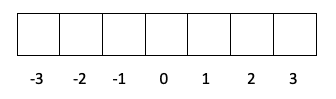
સ્તર d -> l એ 2 છે, તેથી m -2, -1, 0, 1 અને 2 હોઈ શકે છે.

સ્તર f -> l ની કિંમત 3 છે, તેથી m -3, -2, -1, 0, 1, 2 અને 3 હોઈ શકે છે.

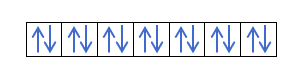
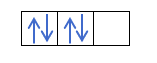
તમે પહેલેથી જ જાણો છો કે ભ્રમણકક્ષાઓ કેવી રીતે ભરાય છે, તેથી ક્વોન્ટમ નંબર m એ છિદ્રનું મૂલ્ય હશે જ્યાં છેલ્લે દોરેલું ઇલેક્ટ્રોન છે. શું તમને આ ઉદાહરણ પહેલાથી યાદ છે?:

આ કિસ્સામાં, m -1 હશે, કારણ કે p શેલ (3 ભ્રમણકક્ષા) માં, જો ત્યાં 4 ઇલેક્ટ્રોન હોય, તો છેલ્લું ભરવાનું પ્રથમ ભ્રમણકક્ષાનું નકારાત્મક હશે.

ક્વોન્ટમ નંબર એસ. ક્વોન્ટમ નંબર s માત્ર worth અને -½ ની કિંમત હોઈ શકે છે. જો દોરેલું છેલ્લું ઇલેક્ટ્રોન હકારાત્મક છે, એટલે કે, તીર ઉપર છે, તો s be હશે. બીજી બાજુ, જો ભ્રમણકક્ષા ભરવા માટેનું છેલ્લું ઇલેક્ટ્રોન નકારાત્મક છે, એટલે કે, તીર નીચે તરફ નિર્દેશ કરીને, s -½ હશે.

કસરતો અને ઉદાહરણો

હા, અમે પહેલેથી જ જાણીએ છીએ કે આ બધી ઘણી બધી માહિતી છે, પરંતુ તમે કેટલાક ઉદાહરણો સાથે તેને વધુ સારી રીતે સમજી શકશો. અહીં અમે જાઓ!

1 ઉદાહરણ

સેલેનિયમ (સે) -> અણુ નંબર: 34

અમે ઇલેક્ટ્રોન રૂપરેખાંકન લખીએ છીએ. અમે મોલર ડાયાગ્રામ મુજબ ઇલેક્ટ્રોન રૂપરેખાંકન લખી રહ્યા છીએ, ધ્યાનમાં લેતા કે s, p, d અને f ભ્રમણકક્ષામાં અનુક્રમે 2, 6, 10 અને 14 ઇલેક્ટ્રોન છે. અમે ઇલેક્ટ્રોનની સંખ્યા ઉમેરીને રૂપરેખાંકન લખી રહ્યા છીએ, જે ઘાતાંક તરીકે લખાયેલ છે.

1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁴

4p ભ્રમણકક્ષા ભરાતી નથી, કારણ કે ઇલેક્ટ્રોન 36 સુધી ઉમેરાશે, અમે 4p મૂકતા નથી⁶પરંતુ 4p⁴.

અમે ક્વોન્ટમ સંખ્યાઓ બહાર કાીએ છીએ. આ કરવા માટે, આપણે વેલેન્સ અથવા વિભેદક ઇલેક્ટ્રોન પર નજર કરીએ છીએ, એટલે કે, છેલ્લું ઇલેક્ટ્રોન કે જેણે ભ્રમણકક્ષા ભરી છે. આ કિસ્સામાં, અમે 4p પર જોશું⁴.
- મુખ્ય ક્વોન્ટમ નંબર. ભરવાનું છેલ્લું ઉર્જા સ્તર 4 હતું.

n = 4