ઇજિપ્તના સામ્રાજ્યની આંકડાકીય દુનિયા આકર્ષક છે. આજે આપણે સંખ્યાઓ વાંચી અને લખી શકીએ છીએ જેમ કે તેઓએ કરી હતી. શું તમે તેમને પણ લખતા શીખવા માંગો છો? વાંચતા રહો અને તમને બધી ચાવીઓ મળી જશે.
પ્રથમ વસ્તુ જે આપણે કરવી જોઈએ તે છે એક તરફ હાયરોગ્લિફમાં સંખ્યાઓના પ્રતિનિધિત્વ વચ્ચેનો તફાવત, જેનો ઉપયોગ પથ્થરમાં કોતરણી માટે કરવામાં આવ્યો હતો અને જે આપણે લખવાનું શીખીશું, અને બીજી બાજુ વંશવેલોમાં રજૂઆત , જે તે ખૂબ જ અલગ હતું અને તે પ્રખ્યાત પાપરી પર દૈનિક લખવા માટે વપરાતું હતું.
આજે પણ કોઈ એવા પ્રાચીન દસ્તાવેજ શોધી શકે છે જે ગણિતનું વધારે જ્ knowledgeાન દર્શાવે છે, પરંતુ ગણિત પ્રત્યે સૈદ્ધાંતિક અભિગમથી અભ્યાસ કરવાની તેમની ઈચ્છા પ્રશંસાને પાત્ર છે.
હકીકત એ છે કે લેખકો તેમની કથામાં તેમની પોતાની સંસ્કૃતિને વિસ્તૃત કરવા માટે હોવા છતાં, મહાન ગ્રીક લેખકોએ ઇજિપ્તવાસીઓને ભૂમિતિ અથવા અંકગણિત જેવા ઘણા ગાણિતિક શાખાઓમાં શિક્ષકો તરીકે ટાંક્યા હતા.
ઇજિપ્તવાસીઓએ મિડલ કિંગડમ ઓફ ઇજિપ્તથી આ સંખ્યાઓનો ઉપયોગ કર્યો હતો, જોકે પાપ્યરી પર રોજ લખતી વખતે તેનો ખરેખર ઓછો ઉપયોગ થતો હતો. આ સમયથી, વંશવેલોનો ઉપયોગ કરવામાં આવ્યો, એક લેખન પ્રણાલી કે જે શાસ્ત્રીઓને ખૂબ ઝડપથી લખવાની મંજૂરી આપે છે.
જો કે, જ્યારે પથ્થરમાં કોતરણીની વાત આવી ત્યારે આ સંકેતલિપીનો ઉપયોગ કરવામાં આવ્યો હતો.
અમે 1799 માં નેપોલિયન બોનાપાર્ટ દ્વારા આદેશિત એક અભિયાનને આભારી હાયરોગ્લિફિક્સની ભાષા શીખીએ છીએ. આવા અભિયાનમાં ઇજિપ્તના રોસેટામાં એક મોટો ગ્રેનાઇટ સ્લેબ મળ્યો, જે ઇંગ્લેન્ડ ત્રણ વર્ષ પછી લેશે અને જે આજે બ્રિટિશ મ્યુઝિયમમાં રાખવામાં આવ્યું છે. લંડન ..
તે પથ્થરમાં 3 જુદી જુદી ભાષાઓમાં લખાણો છે: હાયરોગ્લિફિક્સ, ઇજિપ્તની ડેમોટિક અને પ્રાચીન ગ્રીક; રોસેટા સ્ટોન તરીકે ઓળખાય છે.
1822 માં, જીન ફ્રાન્કોઇસ ચેમ્પોલિયન, તેને સમજાવવાનું શરૂ કર્યું અને પછીના વર્ષે થોમસ યંગે પણ તે કાર્યમાં ફાળો આપ્યો. પછીના વર્ષોમાં ઘણા અન્ય લેખકો આ કારણમાં જોડાયા છે, આમ તમામ માનવજાત માટે હાયરોગ્લિફિક્સની ભાષાને સમજવામાં આવી છે.
નિશ્ચિતપણે, ગણિત માટે સૌથી મહત્વનું હેનરિક બ્રુગ્સ છે, કારણ કે 1849 માં તેમણે "ન્યુમેરોરમ અપુડ વેટરસ ઇજિપ્તિયોસ" પ્રકાશિત કર્યું, સમકાલીન ઇતિહાસમાં ઇજિપ્તીયન ગણિતનો અભ્યાસ કરતો પ્રથમ ગ્રંથ ".
ઇજિપ્તની સંખ્યાઓ કેવી રીતે વાંચવી: પ્રતીકો અને મૂલ્ય
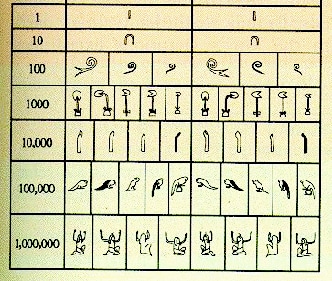
આ હાયરોગ્લિફિક ચિહ્નોનો ઉપયોગ દસની વિવિધ શક્તિઓને રજૂ કરવા માટે કરવામાં આવ્યો હતો:
- વૉકિંગ સ્ટીક. એકમોનું પ્રતિનિધિત્વ કરે છે:
- એક તરીકે. દસનું પ્રતિનિધિત્વ કરો:
- કોઇલ દોરડું. સેંકડોનું પ્રતિનિધિત્વ કરો:
- કમળનું ફૂલ. હજારના એકમોનું પ્રતિનિધિત્વ કરે છે:
- આંગળી. હજારોનું પ્રતિનિધિત્વ કરે છે:
- દેડકા (અથવા ટેડપોલ). સેંકડો હજારોનું પ્રતિનિધિત્વ કરે છે:
(
)
- હે (અનંત અને અનંતકાળના દેવ). એક મિલિયન અથવા અનંતનું પ્રતિનિધિત્વ કરે છે:
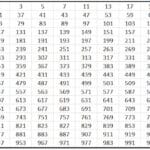
તેને સારી રીતે સમજવા માટે, અમે એક છબી તૈયાર કરી છે 1 થી 100 સુધીના ઇજિપ્તની સંખ્યાઓની સૂચિ સાથે, અને વધુ:
તેથી જો રજૂ કરવાની સંખ્યા 1.322 છે, તો અમે લખીશું
અથવા આપણે પણ લખી શકીએ:કારણ કે તે કોઈપણ ક્રમમાં લખી શકાય છે.
તમારે જાણવું જોઈએ કે 0 અસ્તિત્વમાં નથી (XIII રાજવંશ સુધી, મધ્ય ઇજિપ્તમાં) અને પછી પેપાયરસ પર વંશવેલો પ્રતીક "nfr" નો ઉપયોગ શરૂ થયો અને હાયરોગ્લિફિક રજૂઆતમાં. જો કે આનો અર્થ એ થયો કે ખાલી જગ્યા જે 1 પહેલા અસ્તિત્વમાં છે (અને તે પછી હકારાત્મક અને નકારાત્મક સંખ્યાઓ વચ્ચેની મર્યાદા બની જશે). પરંતુ તે એક અંક ભરવાનું માનવામાં આવતું ન હતું કારણ કે આપણે તેનો ઉપયોગ અમારી અરબી લિપિમાં કરીએ છીએ, કારણ કે આ લેખન પદ્ધતિ ઘણી પાછળથી આવશે.
ઇજિપ્તની સંખ્યાઓને અરબીમાં રૂપાંતરિત કરવાના નિયમો (અમારા નંબરો)
આપણે ઉપરોક્ત સૂત્રને inંધું કરીને ફક્ત અમારા અરબી અંકોમાં અંકોના હાયરોગ્લિફ વાંચી અને અનુવાદિત કરી શકીએ છીએ. ઉદાહરણ તરીકે, જો આપણે પ્રાચીન ઇજિપ્તના પથ્થર પર લખેલી સંખ્યા જોયેઆપણે અનુમાન કરી શકીએ કે તે 45.003 છે.
- તે ડાબેથી જમણે અને versલટું, અને icallyભી (ઉપરથી નીચે) બંને રીતે લખી શકાય છે.
- ઇચ્છિત સંખ્યાને રજૂ કરવા માટે તમને જરૂર હોય તેટલા પ્રતીકોનો ઉપયોગ કરો (1 થી 9 સુધી).
- તેમને બ્લોકમાં જૂથબદ્ધ કરો જ્યાં ઘણા સમાન પ્રતીકો પુનરાવર્તિત થાય છે:
.
- જો તમે ઇજિપ્તીયન લેખક હોવ તો તમારે પથ્થરમાં કોતરણી વખતે જ તેનો ઉપયોગ કરવાની ખાતરી કરવી જોઈએ, પેપ્રી લખવા માટે ઇજિપ્તની ડેમોટિકના વંશવેલો પ્રતીકોનો વધુ સારી રીતે ઉપયોગ કરવો.
- ઇજિપ્તની સંખ્યાઓ સંખ્યાઓ સાથે અથવા પણ રજૂ કરી શકાય છે
- ઓર્ડિનલ્સ બનાવવા માટે: પ્રથમ તેમની પાસે એક અનન્ય પ્રતીક હતું:
. બીજાથી નવમા સુધી તમારે ફક્ત નંબર પર જગ ઉમેરવો પડશે, ઉદાહરણ તરીકે:
. અને દસમી તારીખથી તેઓ "ભરો" નામનું એક ઉમેરીને રચાય છે અને તેમાં આ ફોર્મ છે:
ઇજિપ્તની ગણિત
ઇજિપ્તવાસીઓ ગણિતના ચોક્કસ સ્તર સુધી પહેલેથી જ જાણતા હતા, એ ધ્યાનમાં લેતા કે મધ્ય ઇજિપ્ત સુધી અમારી પાસે પુરાવા નથી કે તેઓ નંબર 0 જાણે છે. સૌથી જૂનું ઇજિપ્તીયન લખાણ જે આપણે જાણીએ છીએ કે ગણિતના ઇજિપ્તીયન ઉપયોગને દર્શાવે છે તે મોસ્કો પેપિરસ છે, જે જૂનો છે. તે સમયથી 2000-1800 બીસી સુધી
પરંતુ યાદ રાખો કે આ માટે તેઓએ હાયરોગ્લિફિક્સમાં ઉપયોગમાં લેવાતા પાત્રો કરતાં અન્ય પાત્રોનો ઉપયોગ કર્યો જે આપણે ઉપર જોયું. ઇજિપ્તવાસીઓએ તેમના દસ્તાવેજોમાં (માત્ર સંખ્યાઓ જ નહીં પરંતુ અન્ય તમામ પાત્રો) તેમની ભાષામાં લખ્યું, ઇજિપ્તીયન ડેમોટિક, જે વંશવેલોમાં લખાયેલું હતું.
આ સિસ્ટમ સાથે, ઇજિપ્તવાસીઓએ ખૂબ ઝડપથી લખ્યું, કારણ કે તેમને સમાન સંખ્યાને રજૂ કરવા માટે ઘણા ઓછા અક્ષરોની જરૂર હતી.
તે કદાચ ખૂબ પહેલાથી છે, પરંતુ આપણે બરાબર જાણીએ છીએ કે 1650 બીસીની શરૂઆતમાં તેઓ સરવાળો અને બાદબાકી, ગુણાકાર અને ભાગાકાર, અંકગણિત અને ભૂમિતિ શ્રેણી, એકમ અપૂર્ણાંક, સંયોજન અને અવિભાજ્ય સંખ્યાઓ, અંકગણિત, ભૌમિતિક અને હાર્મોનિક માધ્યમો અને કેવી રીતે પ્રથમ ક્રમના રેખીય સમીકરણો ઉકેલવા. અને તે પણ 1300 થી. C. બીજો ક્રમ બીજગણિત સમીકરણો (ચતુર્ભુજ) ઉકેલી શકે છે.
પ્રભાવશાળી અધિકાર? ફક્ત મહાન પિરામિડ વિશે વિચારો: શું તમે જાણો છો કે તેઓ તેમની ગાણિતિક ચોકસાઈ માટે પ્રખ્યાત છે? તે ઇજિપ્તની ગણિતની સુસંસ્કૃતતાનો બીજો પુરાવો છે, આ કિસ્સામાં, બાંધકામ માટે.
હાયરોગ્લિફમાં અપૂર્ણાંક વિશે આપણે જાણીએ છીએ , ખુલ્લા મો .ાના રૂપમાં એક આકૃતિ. જાણે કે સંખ્યાને આદર્શ બનાવવી કે જે પોતે રૂપકરૂપે "ખાય છે".
તમે તેની બાજુમાં મુકેલા નંબર દ્વારા તે એક મેચનું પ્રતીક છે. એકમ અપૂર્ણાંકનું પ્રતિનિધિત્વ કરવા માટે, એટલે કે, કોઈપણ સંખ્યા વચ્ચે અપૂર્ણાંક એક, તેમની પાસે બે તૃતીયાંશ (2/3) અને ત્રણ ચતુર્થાંશ (3/4) પણ હતા.
કોતરણીમાં આ એકમના અપૂર્ણાંકને થોડા ફુટમાં ઉમેરવાથી આપણી પાસે બે સંભવિત પરિસ્થિતિઓ છે: પગ લખાણની દિશામાં "ચાલવું" અથવા પગ તેની વિરુદ્ધ જાય છે. જો તેઓ તે તરફ જાય છે જેમાં તે વ્યક્ત કરવામાં આવી રહી છે, તો તેનો અર્થ ઉમેરા છે. જો, બીજી બાજુ, પગ વિરુદ્ધ દિશામાં ચાલે છે, તો તેનો અર્થ છે બાદબાકી.