A prímszámok azok csak 2 elválasztójuk van, mivel csak önmagukban és az egységben, azaz az 1. számban oszthatók, de légy óvatos! Pozitív és negatív számokkal is oszthatók. Mit is jelent ez? Nagyon könnyű. Egy prímszámot, például 2, csak 2 -vel, -2 -vel, 1 -vel és -1 -gyel lehet osztani.
2 -nél több osztóval rendelkező számokat hívnak komponált számokat. Ha vegyünk egy összetett számot, például 10 -et, akkor látni fogjuk, hogy fel tudjuk osztani önmagával és egységével, azaz 10 és 1 között, de 2 és 5 között is. Ezért a 10 összetett szám.
Minden szám prím vagy összetett?
Két van "különleges" számok amelyek nem elsődlegesek és nem összetettek: a 0 és az 1. Miért? Lássuk:
- Az 1 -es szám önmagában (1/1 = 1) és egységben, azaz az 1 -ben (1/1 = 1) osztható. Ahhoz azonban, hogy egy szám prímnek minősüljön, 2 különböző osztóval kell rendelkeznie. Az 1 -es számnak csak egy osztója van, tehát nem prím és nem összetett.
- A 0 nem osztható önmagában, mivel az eredmény határozatlan.
Tehát ha eltávolítjuk a 0 -t és 1 -et a listából, a fennmaradó számok nagy számából, honnan tudjuk, hogy melyek prímek és melyek nem?
Hogyan lehet megtudni, hogy egy szám prímszám -e
A legnormálisabb dolog az, ha elgondolkodunk azon, hogy eldobjuk, vagyis addig próbálkozunk, amíg meg nem találjuk az osztókat. Számológéppel meglehetősen gyors, de ha fejjel lefelé vagy tollal és papírral kell tennünk, akkor a dolgok kissé bonyolulttá válnak. Két módszert tanítunk meg annak megismerésére, hogy egy szám prím vagy sem.
Eratoszthenész szitája
Az Eratosthenes szita a technika a 2 közötti prímszámok megismerésére, ami az első prímszám, és egy bizonyos szám.
Ez a módszer egy táblázat készítéséből és az egész számok többszöröseinek áthúzásából áll. Először megszüntetjük a 2, majd a 3 többszörösét, és így tovább, amíg el nem érjük azt a számot, amely négyzet nagyobb, mint a táblázat utolsó száma.
Mint minden a matematikában, az Eratosthenes szita is egy példával érthető meg a legjobban:
- Táblázatot készítünk 2 és 30 közötti számokkal.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- Kihúzzuk a listából a 2 többszörösét, vagyis áthúzzuk 2 -ről 2 -re: 4, 6 stb. Vigyázz! A 2 -t, amely csak maga és az 1 között osztható fel, nem húzzuk át, mivel ez egy prímszám.
| 2 | 3 | 5 | 7 | 9 | |||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 |
- Felvesszük a következő számot, a 3 -at, és ellenőrizzük, hogy a négyzet kisebb, mint a táblázat legnagyobb száma. Ahogy 32 <30, folytatjuk a szitával, és áthúzzuk annak többszöröseit: 6, 9, 12 ... Az előző lépéshez hasonlóan nem húzzuk át a szintén prímszámú 3 -as számot.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 |
- Az előző lépést megismételjük a táblázat következő számával: 4 -et áthúzzuk, tehát 5. -t vesszük2 <30, áthúzzuk a többszöröseiket.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 |
- A következő számmal folytatjuk áthúzás nélkül: 7. Mint 72 = 49, azaz a 7 négyzet nagyobb, mint a táblázat utolsó száma, a módszer véget ér, és az áthúzás nélküli számok a prímszámok.
- Következtetés. A 2 és 30 közötti prímszámok a következők: 2, 3, 5, 7, 11, 13, 17, 19, 23 és 29.
Az Eratosthenes szita gyors és egyszerű módszer a prímszámok megismerésére, de mi vanmi van, ha a tanulmányozni kívánt szám túl magaspéldául 54657?
Amint megérti, nem lenne praktikus 2-54657 közötti asztalt készíteni, igaz? Mit tehetünk akkor? Nagyon könnyű: használjon oszthatósági kritériumokat.
Oszthatósági kritériumok
Az oszthatósági kritériumok a következők szabályokat annak megállapítására, hogy az egyik szám osztható -e a másikkal anélkül, hogy osztanunk kellene.
Ha tehát ezeket a szabályokat alkalmazzuk, és megfigyeljük, hogy egy szám osztható más számmal önmagán és az egységen kívül, akkor tudni fogjuk, hogy nem prím.
- A 2. szám oszthatóságának kritériuma. Egy szám osztható 2 -vel, ha páros, azaz ha 0, 2, 4, 6 vagy 8 -ra végződik. És itt van egy trükk: mint minden 4 -gyel osztható szám, A 6 vagy 8 is osztható 2 -vel, nem kell ismernünk a többi páros szám oszthatósági kritériumait.
- A 3. szám oszthatóságának kritériuma. Egy szám akkor osztható 3 -mal, ha számjegyeinek összege háromszoros. Lássunk egy példát:
267 -> 2 + 6 + 7 = 15
Mivel a 15 a 3 többszöröse, a 267 osztható 3 -mal.
Ezenkívül, mivel minden 9 -gyel osztható szám 3 -mal is osztható, elég lesz, ha ismerjük ezt a kritériumot.
- Az 5. szám oszthatósági kritériuma. Egy szám osztható 5 -tel, ha 0 -ra vagy 5 -re végződik.
- A 7. szám oszthatóságának kritériuma Annak megállapításához, hogy egy szám osztható -e 7 -gyel, ki kell vonnunk az utolsó számjegy nélküli számot és az utolsó számjegy kétszeresét. Ha a kapott szám 0 vagy 7 többszöröse, akkor a kezdeti szám osztható 7 -tel. Ezt jobban megérti egy példával, térjünk rá!
378 -> 37 − (8 × 2) = 37 − 16 = 21
Mivel a 21 a 7 többszöröse, a 378 osztható 7 -mal.
- A szám oszthatóságának kritériuma 11. Ha kivonjuk a páros számok összegét és a páratlan számok összegét, és a kapott szám 0 vagy 11 -es többszöröse, ez azt jelenti, hogy a vizsgált szám osztható 11 -gyel. egy példa:
8591 -> (8 + 9) − (5 + 1) = 17 − 6 = 11
Mivel a 11 a 11 többszöröse, a 8591 osztható 11 -mal.
És ennyi! Most rajtad a sor: tudod már, hogyan kell kiszámítani, ha ez a magas szám, az 54657 prímszám?
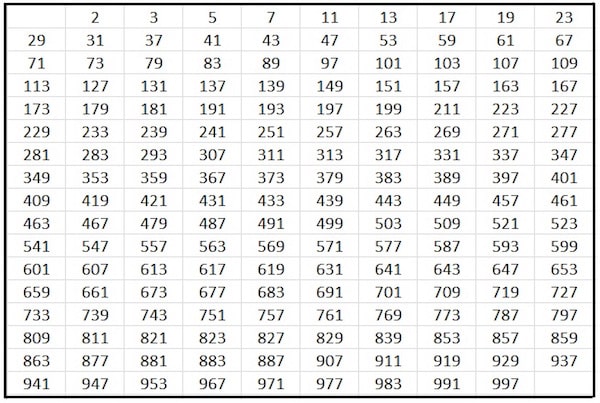
Prímszámok listája 1 és 10.000 XNUMX között
Végül, ha az 1-10.000 1 közötti prímszámok listáját keresi, például 100-1 vagy 1.000-XNUMX, itt egy teljes és frissített lista:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919