Po atomskem modelu Nielsa Bohra so protoni in nevtroni atoma v jedru, elektroni pa okoli njega. Čeprav ne moremo natančno vedeti, kje je elektron, obstajajo območja, kjer ga najverjetneje najdemo, atomske orbitale. In kako lahko določimo te orbitale? Zelo preprosto, z uporabo kvantnih števil.
Kakšne so kvantne številke?
Obstajajo 4 kvantna števila. Trije od njih nam dajejo informacije o tem, kje se nahaja elektron določenega atoma, torej nam dajo podatke o orbiti. Po drugi strani pa nam četrto kvantno število ne pove, kje je elektron, ampak kako. Vam še vedno ni čisto jasno glede tega? Pojdi!
- Glavno kvantno število (n). To je zadnja raven energije, ki jo je treba zapolniti, in označuje velikost orbite in s tem razdaljo med jedrom in elektronom. Zakaj? Zelo enostavno. Večja kot je orbitala, bolj lahko je elektron od jedra atoma.
- Azimutno ali sekundarno kvantno število (l). Označite obliko orbite.
- Magnetno kvantno število (m). Označuje orientacijo orbite.
- Spin kvantno število (s). Povejte, v katero smer se elektron vrti.
Enostavno kajne? Gremo k pomembnemu!
Kako izhajajo kvantna števila
Če želite dobiti kvantne številke, morate slediti 2 preprostim korakom:
- Napišite elektronsko konfiguracijo.
- Pridobite kvantna števila iz diferencialnega elektrona (zadnjega, ki zapolnjuje orbitalno).
Elektronska konfiguracija
Začnemo s 1. korakom, napišemo elektronsko konfiguracijo. Kako? Za to obstajata dva načina, pojdimo k temu!
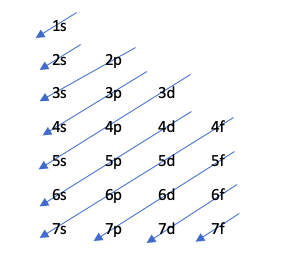
Moellerjev diagram
Ta tehnika prikazuje vrstni red zapolnitve orbitalov po naslednji risbi:
Ta diagram je podrejen Aufbauovemu načelu, ki zagovarja, da orbitale zapolnijo naraščajoči vrstni red energije, to je, da se bo orbitala z najmanj energije napolnila prej.
Če želite ugotoviti, katera orbita ima več energije, se izvede operacija n + l. Če ta operacija za dva različna atoma povzroči enako število, bo imel tisti, pri katerem je število n večje, več energije. Z drugimi besedami, v primeru neodločenega izida se najprej zapolni tisti z najmanjšim številom n. Poglejmo to s primerom:
4p: n + l -> 4 + 1 = 5
5s: n + l -> 5 + 0 = 5
Ker je pravilo n + l enako, se zapolni 4p prej, ker je njegovo število n manjše.
Model jedra
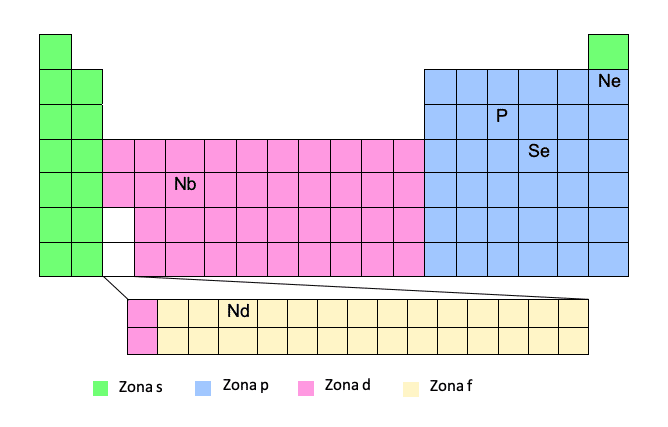
Za pridobitev elektronske konfiguracije po tem modelu morate zelo dobro poznati periodni sistem. Če imamo v tabeli atomsko številko in položaj elementa, je to kos pogače!
Ta metoda velja za poenostavljeno metodo, saj omogoča, da ni treba zapisati celotne konfiguracije elektronov. Na ta način lahko v oklepaje zapišemo ime elementa žlahtnega plina, nato pa pot od tega žlahtnega plina do zadevnega elementa. Poglejmo primer:Tako bomo zapisali pot ob upoštevanju številke obdobja (vrstica periodnega sistema) in "cone" in ko bomo zapisali elektronsko konfiguracijo, bomo izvlekli kvantna števila.
Fosfor (P) bo zapisan iz prejšnjega žlahtnega plina, to je Neona:
P -> [Ne] 3s23p3
Seveda morate biti pri tej metodi previdni, saj sta coni d in f posebni coni. Med potjo v cono d ne vnesemo številke obdobja (vrstice), temveč številko obdobja minus ena. Enako se zgodi s področjem F, ne bomo vpisali številke obdobja, ampak število obdobja minus dva. Bolje boste razumeli z nekaj primeri:
Nb -> [Kr] 5s14d4
Čeprav je v obdobju 5, ko smo v coni d, odštejemo 1.
Nd -> [Xe] 6s24f14
Čeprav je v obdobju 6, ko smo v coni f, odštejemo 2.
Izjeme pri elektronski konfiguraciji
Elektronska konfiguracija ima nekaj posebnih vidikov, ki lahko, če se jih ne zavedate, privedejo do velikih podajalnikov glave. Ampak ne širite panike! Povedali vam bomo!
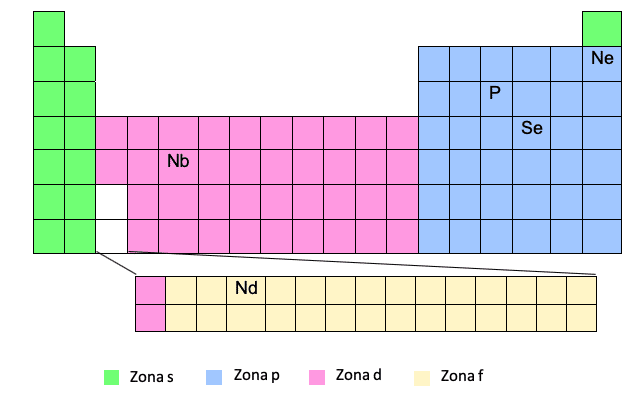
Cona F.
Cona F se pojavi na dnu periodnega sistema, vendar je dejansko "vgrajena" v vrzel, ki jo vidimo v beli barvi, to je med prvim in drugim elementom zadnjih dveh vrstic cone D.
Vidiš? Zato moramo včasih, ko moramo zapisati elektronsko konfiguracijo elementa v coni F, na primer Nd, postaviti elektron v cono D ustrezne ravni glede na tisti element v coni D, ki je pred vstopom cona F.
Ce -> [Xe] 6s25d14f1
Skupina 6 in skupina 11
Prehodne kovine skupine 6 in skupine 11 imajo v svojih zadnjih lupinah 4 oziroma 9 elektronov. Zato se za stabilnejši element s -orbita vzbudi in izgubi elektron, ki preide na naslednjo orbito, d. Na ta način bo s -orbitala ostala z elektronom; in d s 5, če je element skupine 6, ali z 10, če je element skupine 11.
Tukaj je primer:
Ag -> [Kr] 5s24d9
Očitno bi bila to elektronska konfiguracija srebra (Ag). Vendar pa izguba elektrona s s -orbite izgleda takole:
Ag -> [Kr] 5s14d10
Vendar obstajajo izjeme od tega pravila, na primer volfram (skupina 6), ki ima 2 elektrona v s -orbiti in 4 v d -orbiti.
Ampak ne skrbite! Najpogostejši (Cr, Cu, Ag in Au) se držijo tega pravila.
Ali razumeš? No. To je vse, kar morate vedeti o konfiguraciji elektronov. Pojdimo na kvantne številke!
Kako priti do kvantnih števil
Da bi dobili kvantne številke, moramo vedeti, koliko elektronov se prilega v vsako orbitalno lupino, pri tem pa upoštevati, da 2 elektrona ustrezata orbiti.
- Plast s. Ima samo eno orbito, zato lahko sprejme 2 elektrona.
- Plast str. Ima 3 orbitale, zato je prostora za 6 elektronov.
- Plast d. Ima 5 orbitalov, zato lahko sprejme 10 elektronov.
- Plast f. Ima 7 orbitalov, to pomeni, da ima 14 elektronov.
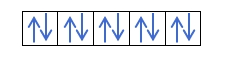
Zdaj, ko razumete, da sta v vsaki orbiti 2 elektrona, bi morali poznati Hundovo pravilo. To pravilo pravi, da pri polnjenju orbitalov istega podnivoja ali lupine, na primer p lupine, elektroni napolnijo orbito v eno smer (pozitivno) in nato v drugo (negativno). Ali ga želite videti s primerom?
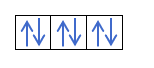
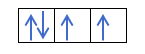
Če imamo 2p4, to je 2p orbitala s 4 elektroni, se ne bo tako zapolnila:
Napolnila se bo tako:
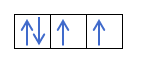
Ali razumete? Super, poglejmo, kako izračunati številke:
- Kvantna številka n. To število sovpada s številko zadnje ravni konfiguracije elektronov. Na primer, če se konfiguracija elektronov konča s 4 s2, glavno kvantno število bo 4.
- Kvantna številka l. Ta številka je odvisna od zadnje napolnjene plasti.
- Plast s -> l = 0
- Plast p -> l = 1
- Plast d -> l = 2
- Plast f -> l = 3
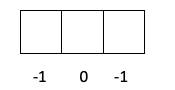
- Kvantno število m. Število m je lahko katera koli vrednost med -l do + l, zato bo odvisno od podnivoja, v katerem je diferencialni elektron, torej od tega, ali je s, p, d ali f. Kako izračunati to število je nekoliko bolj zapleteno, poglejmo to z nekaj risbami:
- Plast s -> Kot smo videli, je l vreden 0, zato je lahko m vreden le 0.
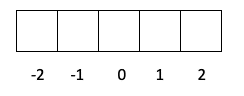
- Sloj p -> L je vreden 1, zato je m lahko -1, 0 ali 1.
- Plast d -> l je 2, zato je m lahko -2, -1, 0, 1 in 2.
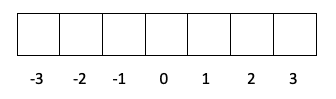
- Plast f -> l je vredna 3, zato je m lahko -3, -2, -1, 0, 1, 2 in 3.
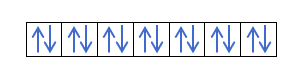
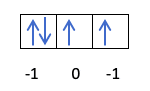
Že veste, kako so orbitale zapolnjene, zato bo kvantno število m imelo vrednost luknje, kjer je zadnji vlečeni elektron. Se spomnite tega primera od prej?:
V tem primeru bo m -1, saj bi v lupini p (3 orbitale), če so 4 elektroni, zadnji, ki bi ga zapolnili, negativen prve orbite.
- Kvantno število s. Kvantno število s je lahko vredno samo ½ in ½. Če je zadnji vlečeni elektron pozitiven, torej puščica navzgor, bo s ½. Po drugi strani pa, če je zadnji elektron, ki je zapolnil orbito, negativen, torej s puščico navzdol, bo s -½.
Vaje in primeri
Da, že vemo, da je vse to veliko informacij, vendar jih boste bolje razumeli z nekaj primeri. Tukaj smo!
Primer 1
Selen (Se) -> Atomska številka: 34
- Zapišemo elektronsko konfiguracijo. Elektronsko konfiguracijo pišemo po Moellerjevem diagramu, pri čemer upoštevamo, da imajo s, p, d in f orbitale 2, 6, 10 oziroma 14 elektronov. Konfiguracijo pišemo z dodajanjem števila elektronov, ki je zapisano kot eksponent.
1s22s22p63s23p64s23d104p4
Ker se 4p orbitala ne napolni, ker bi elektronov seštelo 36, ne postavimo 4p6ampak 4p4.
- Odstranimo kvantne številke. Če želite to narediti, si oglejte valenčni ali diferencialni elektron, to je zadnji elektron, ki je zapolnil orbitalno. V tem primeru bomo pogledali 4p4.
- Glavno kvantno število. Zadnja zapolnjena raven energije je bila 4.
n = 4
- Sekundarno kvantno število. Zadnja energetska podnivo, ki jo je bilo treba zapolniti, je bila p orbitala.
l = 1
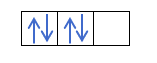
- Magnetno kvantno število. Če črpamo elektrone, bo zadnja zapolnjena prva orbita p -lupine.
m = -1
- Spin kvantno število. Zadnji elektron, ki zaseda p -orbito, ima puščico navzdol.
s = -½
Primer 2
Zlato (Au) -> [Xe] 6s14f145d10
- Glavno kvantno število -> n = 5
- Sekundarno kvantno število -> l = 2
- Magnetno kvantno število -> m = 2
- Spin kvantno število -> s = -½
In to je vse! Zdaj ste na vrsti, bi lahko naredili elektronsko konfiguracijo in dobili kvantne številke naslednjih elementov?:
Cr(24), Rb(37), Br(35), Lu(71), Au(79)