Mga numero ng Egypt mula 1 hanggang 100

Ang kamangha-manghang mundo ng Empire ng Egypt ay kamangha-manghang. Ngayon ay maaari nating basahin at isulat ang mga bilang tulad ng ginawa nila. Nais mo bang malaman na isulat din ang mga ito? Patuloy na basahin at makakakuha ka ng lahat ng mga susi.

Ang unang bagay na dapat nating gawin ay isang pagkakaiba sa pagitan ng representasyon ng mga numero sa hieroglyphs sa isang banda, na ginamit para sa kanilang pag-ukit sa bato at kung alin ang matutunan nating isulat, at sa kabilang banda ang representasyon sa hieratic , kung saan ito ay ibang-iba at ang dating nagsusulat araw-araw sa tanyag na papyri.

Kahit na ngayon ay makakahanap ang ilang mga sinaunang dokumento na nagpakita ng mas higit na kaalaman sa matematika, ngunit ang kanyang pagkasabik sa pag-aaral mula sa isang teoretikal na diskarte sa matematika ay karapat-dapat sa paghanga.

Sa kabila ng katotohanang pinalalaki ng mga may-akda ang kanilang sariling kultura sa kanilang pagsasalaysay, binanggit ng dakilang mga may-akdang Griyego ang mga Egypt bilang mga guro sa maraming disiplina sa matematika tulad ng geometry o arithmetic.

Ginamit ng mga taga-Egypt ang mga bilang na ito mula pa noong Gitnang Kaharian ng Egypt, kahit na talagang hindi gaanong ginagamit ito sa pagsulat araw-araw sa papyri. Dahil sa oras na ito ang hieratic ay ginamit na, isang sistema ng pagsulat na pinapayagan ang mga eskriba na magsulat nang mas mabilis.

Gayunpaman, pagdating sa larawang inukit sa bato ang mga cryptogram na ito ay ginamit.

Nalaman natin ang wika ng hieroglyphics salamat sa isang ekspedisyon, na pinamunuan ni Napoleon Bonaparte, noong 1799. Natuklasan ng naturang ekspedisyon ang isang malaking granite slab sa Rosetta, Egypt, na tatagal ng tatlong taon ang England at kung saan ngayon ay nakalagay sa British Museum sa London.

Ang batong iyon ay may mga teksto sa 3 magkakaibang wika: hieroglyphics, Egypt demotic, at ancient Greek; kilala bilang Rosetta Stone.

Noong 1822, si Jean François Champollion, ay nagsimulang tukuyin ito at sa sumunod na taon ay nag-ambag din si Thomas Young sa gawaing iyon. Sa mga nagdaang taon maraming iba pang mga may-akda ang sumali sa dahilan, sa gayon ay nai-decipher ang wika ng hieroglyphics para sa lahat ng sangkatauhan.

Tiyak, ang pinakamahalaga para sa matematika ay si Henrich Brugsch, mula pa noong 1849 ay nai-publish niya ang "Numerorum apud Veteres Aegyptios", ang kauna-unahang kasunduan na nag-aaral ng mga matematika ng Egypt sa Contemporary History ".

Paano Basahin ang Mga Numero ng Ehipto: Mga Simbolo at Halaga

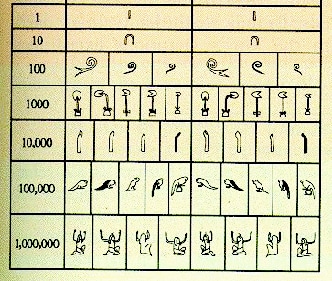
Ang mga palatandaang hieroglyphic na ito ay ginamit upang kumatawan sa iba't ibang kapangyarihan ng sampu:

• Tungkod. Kinakatawan ang mga unit:
• Asa. Kinatawan ang sampu:
• Coiled lubid. Kumakatawan sa daan-daang:
• Bulaklak ng Lotus. Kinakatawan ang mga yunit ng isang libo:
• Daliri. Kinakatawan ng sampu-sampung libo:                       
• Palaka (o tadpole). Kumakatawan sa daan-daang libo:  ()
• Heh (diyos ng kawalang-hanggan at kawalang-hanggan). Kumakatawan sa isang milyon o kawalang-hanggan:

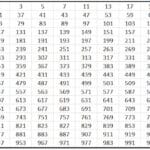
Upang maunawaan ito nang maayos, naghanda kami ng isang imahe na may isang listahan ng mga numero ng Egypt mula 1 hanggang 100, at higit pa:

Kaya't kung ang bilang na kumakatawan ay 1.322, magsusulat kami

O maaari rin kaming magsulat:dahil maaari itong maisulat sa anumang pagkakasunud-sunod.

Dapat mong malaman na 0 wala sa hieroglyphic representation. Bagaman nangangahulugan ito ng walang laman na puwang na mayroon bago ang 1 (at na sa paglaon ay magiging limitasyon sa pagitan ng positibo at negatibong mga numero). Ngunit hindi ito isinasaalang-alang upang punan ang isang digit habang ginagamit namin ito sa aming script sa Arabe, dahil ang sistemang pagsulat na ito ay darating pa sa paglaon.

Mga panuntunan para sa pag-convert ng mga numero ng Egypt sa Arabic (aming mga numero)

Maaari nating basahin at isalin ang mga numerong hieroglyph sa aming mga numerong Arabiko sa pamamagitan lamang ng pag-invert ng pormula sa itaas. Kung nakikita natin ang isang numero na nakasulat sa isang bato mula sa Sinaunang Egypt, halimbawamahihinuha natin na ito ay 45.003.

• Maaari itong maisulat kapwa mula kaliwa hanggang kanan at kabaligtaran, at patayo (itaas hanggang ibaba) din.
• Gumamit ng maraming mga simbolo na kailangan mo (mula 1 hanggang 9) upang kumatawan sa nais na numero.
• Pangkatin ang mga ito sa mga bloke kung saan maraming ng parehong mga simbolo ang inuulit: .
• Kung ikaw ay isang eskriba ng Ehipto dapat mong siguraduhin na gamitin lamang ang mga ito kapag nakaukit sa bato, upang masulat ang papyri na mas mahusay na gamitin ang mga hieratic na simbolo ng demotic na Ehipto.
• Ang mga numero ng Egypt ay maaaring kinatawan ng mga numero o din
• Upang bumuo ng mga ordinal: para sa una ay mayroon silang natatanging simbolo: . Mula sa pangalawa hanggang ikasiyam kailangan mo lamang magdagdag ng isang pitsel sa numero, halimbawa:. At mula sa ikasampu pasulong nabubuo ang mga ito sa pamamagitan ng pagdaragdag ng isang tinatawag na "punan" at mayroon itong form na ito:

Ehipto matematika

Alam na ng mga Egypt ang matematika sa isang tiyak na antas, isinasaalang-alang na wala kaming ebidensya hanggang sa Gitnang Ehipto na alam nila ang bilang 0. Ang pinakalumang teksto ng Ehipto na alam namin na nagpapakita ng paggamit ng matematika ng Ehipto ay ang Moscow Papyrus, na nagsimula pa mula sa oras na iyon hanggang sa mga taon 2000-1800 BC

Ngunit tandaan na para dito gumamit sila ng ibang mga character kaysa sa ginamit sa hieroglyphics na nakita natin sa itaas. Ang mga taga-Egypt sa kanilang mga dokumento ay nagsulat (hindi lamang mga numero ngunit lahat ng iba pang mga character) sa kanilang wika, ang demonyo ng Egypt, na nakasulat sa hieratic.

Sa sistemang ito, ang mga taga-Egypt ay sumulat nang mas mabilis, dahil kailangan nila ng mas kaunting mga character upang kumatawan sa parehong numero.

Marahil ay mas maaga ito, ngunit alam natin eksakto na noong 1650 BC alam nila ang tungkol sa pagdaragdag at pagbabawas, pagpaparami at dibisyon, serye ng aritmetika at geometry, mga praksiyon ng yunit, tambalan at pangunahing mga numero, arithmetic, geometric at harmonic na paraan, at kung paano upang malutas ang unang order ng mga linear equation. At gayun din mula 1300 a. C. maaaring malutas ang pangalawang pagkakasunud-sunod ng mga equation algebraic (quadratic).

Kahanga-hanga di ba? Isipin lamang ang magagaling na mga piramide: Alam mo bang sikat sila sa kanilang katumpakan sa matematika? Ang mga ito ay isa pang katibayan ng pagiging sopistikado ng Egypt na matematika na inilapat, sa kasong ito, sa konstruksyon.

Tungkol sa mga praksiyon sa mga hieroglyph na alam natin , isang pigura sa anyo ng isang bukas na bibig. Tulad ng kung pag-idealize ang isang bilang na "kumakain" mismo ng talinghaga.

Sumisimbolo ito ng isang tugma ng numero na inilagay mo sa tabi nito. Bilang karagdagan sa kumakatawan sa mga praksyon ng yunit, iyon ay, ang maliit na bahagi sa pagitan ng anumang numero, mayroon din silang dalawang katlo (2/3) at tatlong pang-apat (3/4).

Ang pagdaragdag ng mga maliit na bahagi ng yunit na ito sa ilang mga paa sa isang pag-ukit ay mayroon kaming dalawang mga posibleng sitwasyon: ang mga paa ay "lumalakad" sa direksyon ng pagsulat o ang mga paa ay laban dito. Kung pupunta sila sa panig kung saan ito ay ipinahayag, ang ibig nilang sabihin ay karagdagan. Kung, sa kabilang banda, ang mga paa ay naglalakad sa kabaligtaran na direksyon, nangangahulugan ito ng pagbabawas.